M.Sc. Benedikt Grüger

Power grid dynamics
+49 (0) 6151 16-21724
fax +49 (0) 6151 16-21712
S3|10 310
Landgraf-Georg-Str. 4
64283 Darmstadt
Research Interest
General Research Interest:
- Dynamical models of power grids
- Harmonic interaction in inverter-dominated power grids
- Non-linear coupled systems
Research Project:
Our research investigates vulnerabilities of power grids relevant to cyber-attack resilience focusing on non-linear dynamical phenomena. Studying universal features in transient dynamics numerically, we aim to gain a theoretical understanding of power grids' response to disturbances. Special emphasis is put on voltage dynamics in distribution grids and the interaction of inverter controls with the power grid. The gained insights are then used to formulate novel cyber-attack scenarios. Furthmore, we develop corresponding application-oriented defense strategies in collaboration with different grid operators. Overall, the research applies theoretical concepts from complex systems theory and statistical physics to the energy sector trying to contribute to today's power grid stability.
Open theses
Supervisor: Benedikt Grüger
Earliest start: immediately
Type: Master Thesis
Since modern power systems increasingly depend on power electronic converters accurate dynamical stability studies of distribution grids become more necessary. Reduced-order models are expected to contribute to velocity and scalability of simulation frameworks. Order reduction is often based on time-scale separation arguments: Fast inner control loops and slower outer dynamics uncouple. However, this assumption may break down during transient events caused by large perturbations leading to erroneous conclusions on stability.
This thesis explores the dynamical interaction of controllers in grid-following converters. Using both a full-order Simulink model and reduced-order models, the system’s response to disturbances—such as voltage fluctuations at the point of common coupling—is analyzed. With this, we explore which type of perturbations lead to instability. Particular attention is given to the validity of time-scale separation and how different control layers influence one another during transients. The existing code base, developed in Matlab and Julia, is extended to support this analysis.
The research contributes to a deeper understanding of converter behavior under perturbations and informs the development of improved modelling approaches.
The following papers are considered a good starting point:
- Synchronization stability and multi-timescale analysis of renewable-dominated power systems (Ma et al. 2023)
- Voltage Dynamics of Current Control Time-Scale in a VSC-Connected Weak Grid (Zhao et al. 2016)
- Understanding Small-Signal Stability of Low-Inertia Systems (Markovic et al. 2021)
Supervisor: Benedikt Grüger
Earliest start: immediately
Type: Bachelor Thesis
In the AC transmission grid, complex interactions lead to interesting but unwanted dynamical phenomena. A key ingredient of stable electric power transport is phase angle stability which is at risk, if generators of different grid areas oscillate against each other. This electro-mechanical phenomenon, known as inter-area oscillation with frequencies between 0.1 and 1Hz, can cause . power line tripping, desynchronization, and, in the worst case, blackout. Therefore, it constitutes a natural candidate for cyber-physical attacks, e.g. dynamic load altering attacks. Inter-area oscillations can already be observed in the non-linear coupled swing model, aca Kuramoto model. Despite neglecting voltage dynamics, this model has proven useful in the conceptual understanding of corresponding oscillations modes.
This thesis explores attack-induced inter-area oscillations the coupled swing model. In particular, two different model versions are considered and compared to assess the role of voltage dynamics. Moreover, we are interested in optimal attack design and the role of heterogeneous system parameters. Further steps involve the development of adequate control tuning that can counteract these attacks. The analysis employs methods from linear response theory and dynamical systems. Experience in control theory, complex systems theory, and/or power system engineering is advantageous. Successful completion requires mathematical maturity and robust programming skills in either Python or Julia.
Overall, inter-area oscillations make a fascinating and highly relevant research subject.
- Investigation of impacts on the disturbance propagation in power systems (Semerow et al. 2016)
- Low frequency oscillations in the interconnected system of Continental Europe (Grebe et al. 2010)
- Dynamic Study Model for the interconnected power system of Continental Europe in different simulation tools (Semerow et al. 2015)
Supervisor: Benedikt Grüger
Earliest start: immediately
Type: Master Thesis
With the ongoing large-scale integration of renewable energy sources, distribution grids are increasingly dominated by grid-following converters. Since converter control operates on significantly shorter time scales, evaluating their dynamic stability under varying grid conditions becomes crucial.
In the presence of large disturbances, the non-linear behavior of converter dynamics becomes particularly important. In such cases, stability analysis can be based on the concept of the region of attraction—the set of initial states from which the system returns to its desired operating point without external intervention. Determining this region, however, is computationally demanding, especially for higher-order systems. To address this, several numerical methods have been developed to approximate the boundary of the region of attraction, such as the unstable manifold method and the interval stability method.
This thesis investigates different numerical techniques for approximating the region of attraction boundary for a grid-following converter. In particular, these methods are compared against the standard Monte Carlo approach. Their practical applicability is demonstrated using two lower-order models of grid-following converters.
Overall, this work contributes to ongoing efforts in converter modeling and provides insights into the impact of non-linear dynamics on the stability of future power systems.
- Stability threshold approach for complex dynamical systems (Klinshov, Nekorki, and Kurths 2015)
- Interval stability for complex systems (Klinshov et al. 2018)
- Domain of Attraction’s Estimation for Grid Connected Converters With Phase-Locked Loop (Zhang et al. 2022)
- Dominant Transient Equations of Grid-Following and Grid-Forming Converters by Controlling-Unstable- Equilibrium-Point-Based Participation Factor Analysis (Ma et al. 2024)
Short Bio
- Physics, Bachelor of Science, University of Göttingen (10/2015 - 03/2019)
- Semester abroad, Universidad de la Laguna (09/2017 - 02/2018)
- Physics, Master of Science, University of Göttingen (10/2020 - 02/2023)
- Research associate, Energy Information Networks and Systems Lab, TU Darmstadt (since 07/2023)
Publications
[Conference]
Benedikt Grüger, Florian Steinke:
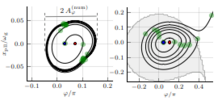
Grid-following Converter Dynamics under Large Sub-synchronous Voltage Fluctuations.
In: IEEE PowerTech 2025, Kiel, Germany, 2025
[Conference]
Adeel Jamal, Benedikt Grüger, Kirill Kuroptev, Michael Wolff, Florian Steinke, Gerd Griepentrog:
Exploring Cyber Threats based on Harmonic Distortions: A Testbed to analyze Attack Scenarios .
In: Energy Conversion Congress & Expo Europe, Darmstadt, 2024